- Bentuk-Bentuk Fungsi Eksponen
Fungsi eksponen dibagi menjadi dua, yaitu:
• Berbentuk f (x) = a x dengan a > 1, a ϵ Ɍ dan x ϵ Ɍ.Fungsi Eksponen f (x) = a x untuk a > 1 disebut sebagai fungsi monoton naik, sebab jika x1 < x2maka ax1 < ax2.Bentuk di atas dapat dinyatakan dalam pertidaksamaan yang lebih umum, sebagai berikut: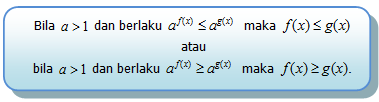
• Berbentuk f (x) = a x dengan 0 < a < 1, a ϵ Ɍ dan x ϵ Ɍ.Fungsi Eksponen f (x) = a x untuk 0 < a < 1 disebut sebagai fungsi monoton turun, sebab jika x1> x2maka ax1 > ax2.Bentuk di atas dapat dinyatakan dalam pertidaksamaan yang lebih umum, sebagai berikut: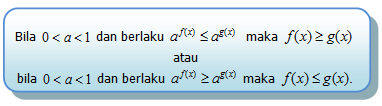
Penerapan Fungsi Eksponen
• Fungsi Pertumbuhan Eksponensialy = b. a x dengan a = 1 + rKeterangan:b = jumlah awal (ketika x = 0)a = faktor pertumbuhan (a > 1)r = laju pertumbuhan per selang waktu T.y = jumlah setelah selang waktu tx = fraksi dengan x = tT• Fungsi Penyusutan Eksponensialy = b. a x dengan a = 1 – rKeterangan:b = jumlah awal (ketika x = 0)a = faktor penyusutan (0 < a < 1)r = laju penyusutan per selang waktu T.y = jumlah setelah selang waktu tx = fraksi dengan x = tT• Fungsi Peluruhan Radioaktifm = m0 × (12)nKeterangan:m = massa setelah selang waktu t.m0 = massa awaln = tTt = selang waktuT = waktu paruh
- Grafik Fungsi Eksponen
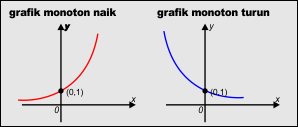
- Contoh soal dan Pembahasan
- Tentukan nilai a jika grafik fungsi f (x) = a x melalui titik:
• P = ( 2, 14)
• Q = (3, 8)
Penyelesaian:
• P = ( 2, 14)
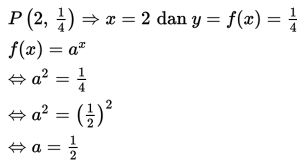 • Q = (3, 8)
• Q = (3, 8)
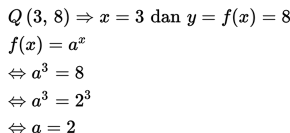
-
Sederhanakanlah!
(3x2 . y 5) ( 3x -8 . y9)
Jawab:
(3x2 . y -5) ( 3x -8 . y9) = (3x2 ) ( 3x -8 ) (y -5) (y9)
(3x2 . y -5) ( 3x -8 . y9) = (3) (-3) (x2 + -8 ) (y -5+9)
(3x2 . y -5) ( 3x -8 . y9) = -9 x-6 y 4
(3x2 . y -5) ( 3x -8 . y9) = -(9y6/ x6)
-
Hitunglah!
Jika f(x) = 2x+1 tentukan nilai dari f(3) dan f(-3)
• P = ( 2, 14)
• Q = (3, 8)
Penyelesaian:
• P = ( 2, 14)
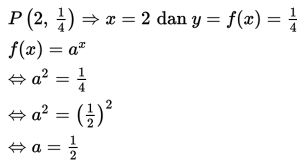
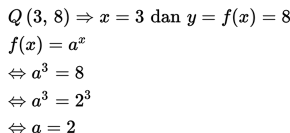
Sederhanakanlah!
(3x2 . y 5) ( 3x -8 . y9)
Jawab:
(3x2 . y -5) ( 3x -8 . y9) = (3x2 ) ( 3x -8 ) (y -5) (y9)
(3x2 . y -5) ( 3x -8 . y9) = (3) (-3) (x2 + -8 ) (y -5+9)
(3x2 . y -5) ( 3x -8 . y9) = -9 x-6 y 4
(3x2 . y -5) ( 3x -8 . y9) = -(9y6/ x6)
(3x2 . y -5) ( 3x -8 . y9) = (3x2 ) ( 3x -8 ) (y -5) (y9)
(3x2 . y -5) ( 3x -8 . y9) = (3) (-3) (x2 + -8 ) (y -5+9)
(3x2 . y -5) ( 3x -8 . y9) = -9 x-6 y 4
(3x2 . y -5) ( 3x -8 . y9) = -(9y6/ x6)
Hitunglah!

Baguss...
BalasHapus